i) 唯一编号法
:如果我们发现某个格子只有一个可用的候选数字,那么这个格子一定是这个数字,这就是唯一数字法,比如下面这个例子中,H5格子中只有一个唯一候选数字3。
ii) 隐式唯一编号方法
如果我们发现某一行、某一列或某一方格中的某个候选数字只出现在一个格子中,那么这个格子一定是这个数字。这就是隐式唯一数法。例如,在下面的例子中,第三列的候选数字 4 只出现在 I3 格子中。
iii) 数字对法
如果我们发现某一行、列或九宫格中有两个格子只用了两个候选数字,那么这两个格子就一定是这两个数字。在这个单元(行、列或九宫格)中,这两个候选数字不会出现在其他格子中。这就是数字对法。如下例中,第一列的 B1 和 G1 的候选数字都是 7 和 8;那么 D1 和 H1 中的候选数字 7 和 8 就可以删除。
iv) 三重链数法
如果我们发现某一行、某一列或者九宫格中有三个格子只用了三个候选数字,那么这三个格子就一定正好是这三个数字。在这个单元(行、列或者九宫格)中,这三个候选数字不会出现在其他格子中。这就是三连数法,如下例所示。
中下九格中,H4、H5、I5三个格子只使用了候选数字2、8、6,因此可以删除G4、G6、I6中出现的8和6。
v) 四链法
如果我们发现某一行、某一列或某一方格中有四个格子只用了四个候选数字,那么这四个格子就一定正好是这四个数字。在这个单元(行、列或方格)中,这四个候选数字不会出现在其他格子中。这就是四链数法;如下例
上图九个方格中间,A5、B5、C4、C5四个格子只用到了数字1、2、3、4;所以可以删除另外四个格子A4、A6、B4、C6中出现的数字1、2、3、4
vi) 隐式数对法
如果我们发现某一行、某一列或者一个九宫格中有两个候选数字只出现在两个格子中,那么这两个格子肯定就是这两个数字,因此可以删除这两个格子中的其他候选数字。这就是隐式数字对法;如下例所示,在 A 行中,只有 A7 和 A8 格子使用了数字 6 和 8;因此可以删除这两个格子中的其他数字 2、5 和 9
vii) 隐式三重链数法
如果我们发现一行、一列或一个九宫格中有三个候选数字只出现在三个格子中,那么这三个格子中肯定就是这三个数字,因此可以删除这三个格子中的其他候选数字。这就是隐式三链数法。例如,在下面的例子中,只有第 8 列的 C8、F8 和 G8 格子使用了数字 1、3 和 4;因此可以删除 F8 格子中出现的其他数字 6、7 和 8。
viii) 隐式四链数法
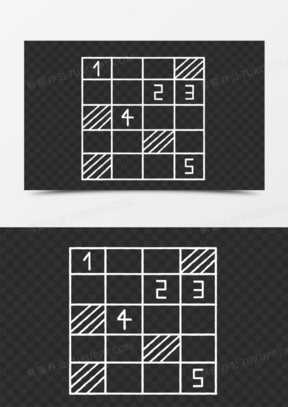
如果我们发现某一行、某一列或者一个九宫格中有两个候选数字只出现在两个格子中,那么这两个格子中肯定就是这两个数字,因此可以删除这两个格子中的其他候选数字。这就是隐式四连环数法。借用四连环数的例子,发现在上面的中间九宫格中,只有 A4、A6、B4、C6 格子使用了 5、6、7、9 这四个数字;因此可以删除它们使用的其他数字 1、2、3、4。
ix) 区域减法
如果我们发现某个单元(行、列、九宫格)上的候选数字完全位于与另一个单元的交点中,那么在另一个单元中,可以将不在交点中的候选数字删除。例如,下面的例子中,第 D 行的所有数字 5 恰好位于左侧中间的九宫格中,因此在这个九宫格中,可以将不在第 D 行的候选数字 5(位于 E3 中)删除。
x) 矩形法
如果某个候选数字只出现在两行(列)中,则可以删除不在该两行(列)中的候选数字。例如,以下示例中,C 行和 F 行中恰好有两个候选数字 3,它们出现在第 1 列和第 8 列中;因此,可以删除第 1 列和第 8 列中但不在 C 行和 F 行中的候选数字 3(A8、D1、D8、I1、I8)。
将其扩展为三行或四行,即可得到高阶矩形法(我也见过将其翻译成3链式和4链式)。同样,在下面的例子中,我们可以删除蓝色候选数字6。
xi) 唯一矩形法
最新加入的是唯一矩形法,它利用了数独结果的唯一性:如果组成矩形顶点的四个格子只使用两个数字,并且同一行或列的格子在同一个格子中,那么这种情况的结果一定不唯一(交换它们使用的数字也能得到合法的数独结果),也一定不是合法的数独情况。基于这个结论,我们得到了两种删除方法:
如下图A3,C3,A9,C9,C3一定不能取候选数1和9(否则结果一定不唯一),所以C3只能取候选数5。
如下图所示,D2 和 F2 中必须有一个单元格的结果为 3,否则 D2、F2、D9、F9 只能是数字 1 和 9,且结果不唯一。
由此,我们可以进一步得出结论,第二列中的 H2 不能为 3(同样,我们可以得出结论,左侧中心网格中的 F3 不能为 3)
xii) 相关数减少方法
通过寻找一串强相关数据产生矛盾来排除候选数字。
如下图所示,第9列中,只有G9和D9的候选数为3,是强相关数据。同样,D4和I4也是强相关的。
另外,D9和D4都用的是同一行的数据3,所以是弱相关的。这样,通过一系列的强相关和弱相关(弱相关可以用强相关代替),
如果我们可以得到一个矛盾链,如下图所示,我们可以通过提示中的逻辑推理排除G6=3(实际上,我们也可以排除I7=3和I8=3)
以下是使用多个候选数字的更复杂的例子:














































